|
 Principe
de la synthèse numérique
directe DDS :
Principe
de la synthèse numérique
directe DDS :
 Architecture
simplifiée du générateur
et principe de fonctionnement
:
Architecture
simplifiée du générateur
et principe de fonctionnement
:
Ce
générateur présente
des caractéristiques très
attractives grâce à une
approche totalement numérique
basée sur le principe de la Synthèse
Numérique Directe ou DDS en anglais.
L'architecture
générale de ce générateur
est illustrée sur la figure
ci-dessous.
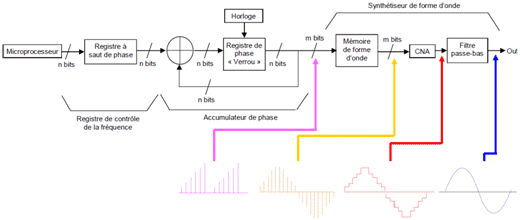
Cliquez sur l'image
ci-dessus pour l'agrandir
Notez
que l'ensemble
des fonctions "registre
à saut de phase",
"additionneur"
et "registre
de phase"
ont été totalement intégrés
dans le
circuit logique programmable CPLD
placé au sein de notre générateur
de fonctions. L'usage d'un tel circuit
fut nécessaire vis à vis
des contraintes du cahier des charges
telles que: des
dimensions réduites,
une
consommation raisonnable et
un cout
de revient attractif.
Une réalisation équivalente
de ce projet à base de
circuits logiques en technologie Fast-TTL
(74Fxxx) aurait demandé un
circuit imprimé deux fois plus
grand, une
bonne poignée de circuits logiques
74Fxxx / 74HCxxx,
une
alimentation de plus forte puissance
pour un
coût final deux fois
plus élevé. Ainsi, de
part l'usage du circuit CPLD,
vous ne trouverez pas les 3 éléments
principaux
de la synthèse numérique
directe représentés
par des circuits intégrés
en logique
TTL sur le schéma
de principe de cet instrument.
Le
point de départ du système
est le microprocesseur chargé
de délivrer la consigne sous
la forme d'un mot binaire
codé sur n bits
(16 pour notre générateur)
constituant ainsi le
registre de chargement.
Dans la réalité et afin
de réduire
le nombre de liaisons
électriques entre
le microcontrôleur et le CPLD,
le transfert des données s'effectue
par liaison
série synchrone nécessitant
seulement que 2
liaisons électriques. Des
registres à décalage
présents dans le CPLD se chargent
ensuite de transformer les données
séries en données parallèles
sur 16 bits nécessaires au registre
à saut de phase
dont
l'appellation sera commentée
un peu plus loin.
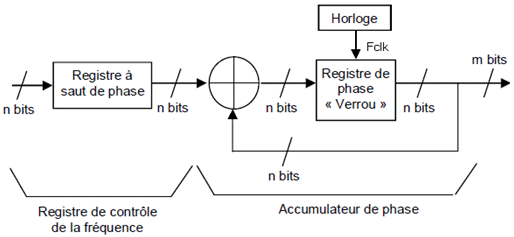
Le
coeur du système est l'accumulateur
de phase dont
le contenu
est recalculé lors de chaque
période
de l'horloge TClk.
L'accumulateur de phase est constitué
d'un
additionneur binaire
sur
n bits et
d'un registre
de phase appelé
aussi
verrou.
Si l'on devait réaliser ces éléments
en technologie TTL, l'additionneur binaire
serait constitué de plusieurs
additionneurs rapides de type 74F283
et le registre de phase par des octuples
verrous de type D tel que des 74F374.
Ainsi,
pour chaque cycle d'horloge :
 la
sortie
de l'additionneur
est stockée dans le
registre de phase. la
sortie
de l'additionneur
est stockée dans le
registre de phase.
 le
contenu
du
registre à saut de phase est
ajouté
au contenu
du
registre de phase. le
contenu
du
registre à saut de phase est
ajouté
au contenu
du
registre de phase.
On
utilise seulement une
partie des n bits de
sortie du registre de phase, soit m
bits
pour constituer le bus
d'adresses de la RAM
(15 pour notre générateur
de A0 à A14) et générer
également l'horloge
secondaire nécessaire
au convertisseur numérique -
analogique. La RAM contient l'information
pour synthétiser la forme d'onde
voulue (sinusoïde, triangle, etc...).
En effet, c'est elle qui convertit
l'information
de
phase en
information d'amplitude.
La
conversion
numérique / analogique
(CNA) peut être réalisée
de différente manière.
Soit on utilise un réseau
de résistances de
type R-2R
, ou bien on fait appel à un circuit
intégré spécialisé
offrant une bien meilleure dynamique
et linéarité. C'est cette
dernière solution qui a été
employée dans notre générateur.
Le CNA permet de délivrer en
sortie la forme d'onde souhaitée
en analogique quantifié (marches
d'escalier).
Le
filtre
passe-bas
sert à
lisser le signal
et supprimer cette allure en marches
d'escalier
due à l'échantillonnage
mais également, il permet d'éliminer les harmoniques
supérieurs
indésirables
générés par l'échantillonnage.
 Fonctionnement
détaillé de l'accumulateur de phase :
Fonctionnement
détaillé de l'accumulateur de phase :
 La
théorie du générateur
de phase :
La
théorie du générateur
de phase :
L'étude
dans le domaine
temporel de
l'accumulateur
de phase
permet de mieux comprendre son principe
de fonctionnement.
L'évolution
du contenu de l'accumulateur de phase
en
fonction du temps
peut
être extrapolée à
une succession de dents
de scie.
En effet à chaque
front montant du signal d'horloge TClk,
le contenu
du registre de phase est augmenté
de la valeur du registre à saut
de phase et ainsi de suite. Dans le cas où la capacité
maximale de
l'accumulateur est atteinte, ce dernier
perd sa retenue (ici le bit n+1 soit
le 16ème bit dans le cadre de
ce projet) mais conserve
le mot binaire présent sur ses
sorties de poids inférieur (bit
1 à n). C'est à cet instant
précis que la dent de scie suivante
prend naissance.
Afin
de fixer les idées, prenons
pour simplifier un accumulateur de phase
de 4 bits
dont
les sorties évoluent entre 0
et 15.
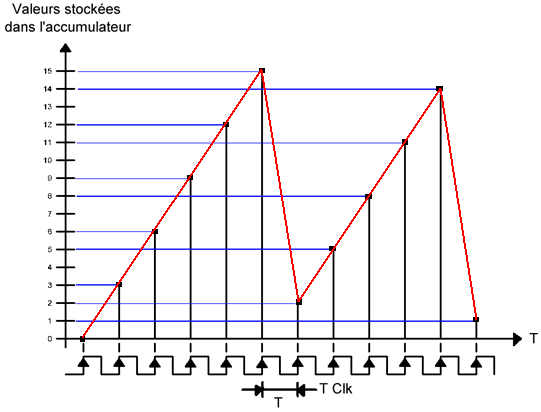
Considérons
arbitrairement que notre
registre à saut de phase
soit positionné sur la
valeur 3 par
le microcontrôleur et
que notre accumulateur de phase soit
initialisé à la valeur
0.
Dans ce cas, à chaque front de
l'horloge, le contenu de l'accumulateur
est incrémenté de 3 en
3 et ainsi de suite tant que la valeur
du registre
à saut de phase reste
identique. La progression de l'accumulateur
sera donc 3 puis 6, 9, 12 et 15 tant
que l'accumulation de phase n'a pas
atteint sa capacité maximale. La valeur
suivante de 15
devrait être
18 mais
comme la capacité
de l'accumulateur n'est que de
4 bits,
la valeur qui succède à
15 correspond aux 4
bits de poids faible de 18
( 18 = 10010 en binaire) soit
2
(2=0010
en binaire). Le comptage continue
alors avec les valeurs 5, 8, 11, 14 jusqu'au
nouveau dépassement de la capacité
de l'accumulateur. Comme précédemment,
la valeur suivant 14 n'est pas 17
(17=10001 en binaire) mais 1
(1
= 0001 = 1 en binaire).
Ainsi,
la
période du signal de sortie correspond
au temps nécessaire mis par l'accumulateur
de phase pour
arriver à
saturation.
Attention dans l'exemple précédent,
la première dent de scie dure
1 un cycle d'horloge supplémentaire
vis à vis de tous les autres
car nous étions
dans la phase de démarrage de
l'accumulateur.
De
la sorte, un
accumulateur de phase sur
n
bits
peut prendre 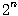 valeurs différentes
dans le cas où le registre
à saut de phase
est initialisé sur sa plus
petite valeur,
c'est à dire 1.
Si le
registre à saut de phase
contient la valeur 2,
il faudra alors
valeurs différentes
dans le cas où le registre
à saut de phase
est initialisé sur sa plus
petite valeur,
c'est à dire 1.
Si le
registre à saut de phase
contient la valeur 2,
il faudra alors
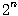 /
2 cycles
d'horloge pour saturer
l'accumulateur de phase. De part cette
progression on peut en déduire
facilement l'équation fondamentale
de la Synthèse Numérique
Directe, à savoir : /
2 cycles
d'horloge pour saturer
l'accumulateur de phase. De part cette
progression on peut en déduire
facilement l'équation fondamentale
de la Synthèse Numérique
Directe, à savoir :
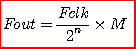
dans
laquelle :
 Fout représente la fréquence
de sortie du bit de poids le plus élevé
de l'accumulateur de phase;
Fout représente la fréquence
de sortie du bit de poids le plus élevé
de l'accumulateur de phase;
 Fclk représente la fréquence
de l'horloge cadençant le registre de
phase;
Fclk représente la fréquence
de l'horloge cadençant le registre de
phase;
 M correspond à la valeur appliquée
au registre à saut de phase (par
le microcontrôleur);
M correspond à la valeur appliquée
au registre à saut de phase (par
le microcontrôleur);

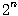 avec
n, le nombre de bits de l'accumulateur. avec
n, le nombre de bits de l'accumulateur.
Dans
le cadre de notre projet, c'est cette
même équation qui est implémentée
dans le microcontrôleur de gestion.
Il est
chargé de positionner le registre
à saut de phase selon la fréquence
désirée sur les bits m
sachant que c'est le bit
de poids fort de l'accumulateur de phase
qui
délivre la plus haute
fréquence.
De
la sorte, le bit de poids fort en sortie du registre
de phase
est appliqué sur le bit de poids
le plus faible
du bus
d'adresse
de la
mémoire RAM
(A0). Les 14
autres sorties du registre de phase
sont des sous-multiples
de fréquence de 2
permettant d'adresser ainsi la mémoire
RAM comme le ferait un
compteur binaire traditionnel à
15 sorties.
Autrement dit, dans la synthèse
numérique directe, le signal
de sortie est subdivisé par un
maximum de 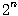 positions.
positions.
La
résolution, c'est à dire
le plus petit pas de fréquence
possible en sortie du générateur
DDS se déduit de l'équation
précédente en remplaçant
M par 1.
Ainsi dans notre projet, sachant que
la fréquence de
l'oscillateur à quartz est de
Fclk=64MHz avec
n=15
bits
et pour M=1
nous obtenons donc une fréquence
Fout = 1953Hz
représentant la
résolution de notre générateur
DDS,
c'est à dire
le plus petit saut en fréquence
possible.
Nous verrons plus loin comment nous
sommes parvenu à obtenir toutes
les fréquences possibles et non
pas seulement des multiples de 1953Hz.
La
limitation théorique pour la
fréquence de sortie Fout est
égale à :
|
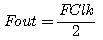
|
obtenue
pour
|
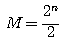
|
Au
delà de cette valeur de M, le
générateur DDS voit sa
fréquence chuter.
De
la sorte,
la
fréquence maximale possible d'un générateur DDS est
égale à la moitié
de la fréquence d'horloge -
théorème de Shannon bien
connu.
Dans
le cadre de ce projet la valeur
maximale de M que
nous pouvons appliquer au générateur
DDS est donc de
16384 correspondant
à une fréquence Fout
maxi de
32MHz,
moitié de notre fréquence
d'horloge à 64MHz.
Cependant,
le théorème de Shannon
n'est
pas la seule limite d'un générateur
DDS.
L'autre paramètre crucial et
souvent mal connu concerne le
temps de propagation
dans le circuit constituant le générateur
DDS. En effet, l'usage de
sommateurs cascadés et les multiples
verrous D-latch
engendrent inévitablement un
temps de propagation dans l'établissement
du signal au sein des circuits.
Et
c'est cette seconde
raison
pour laquelle, l'usage d'un CPLD s'avère
judicieux
car son temps de propagation est
nettement inférieur au temps
proposé par la technologie Fast-TTL.
 La
notion de phase du registre à
saut de phase :
La
notion de phase du registre à
saut de phase :
Essayons
maintenant d'expliciter la
notion de phase dans le cas du registre
à saut de phase.
Nous
savons que tout signal périodique,
sinusoïdal, triangulaire, etc... est
décrit notamment par son amplitude,
sa
fréquence et
sa phase.
Prenons le cas d'une sinusoïde
comme ci-dessous.
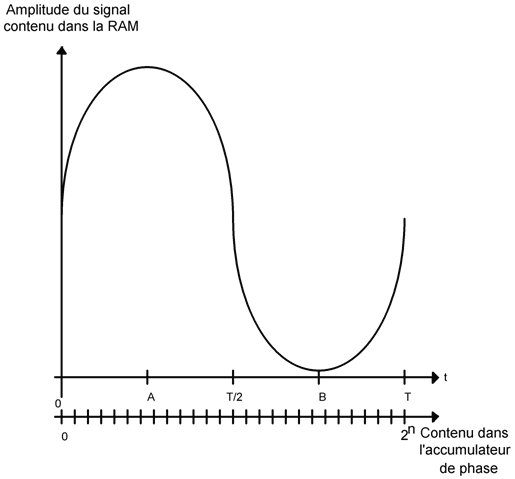
La
phase de n'importe quel signal périodique
représente la
position dans le temps où l'on
se situe dans la période.
Elle s'exprime en degré
et la correspondance avec la période
s'établit
par une règle de trois sachant
que
la phase est à 360° à
l'instant T.
Ainsi, la phase au
point A est à 1/4T soit 90°,
celle du point B
est à 3/4T soit 270°.
Dans la synthèse numérique
directe, le signal de sortie est subdivisé
par un maximum de 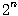 positions.
Le
plus petit saut de phase
est obtenu lorsque M
vaut 1.
Le contenu M du registre à saut
de phase définit
la quantité de phase qui est
ajoutée à
chaque période
d'horloge Fclk,
au contenu
de l'accumulateur de phase. positions.
Le
plus petit saut de phase
est obtenu lorsque M
vaut 1.
Le contenu M du registre à saut
de phase définit
la quantité de phase qui est
ajoutée à
chaque période
d'horloge Fclk,
au contenu
de l'accumulateur de phase.
Les
deux illustrations ci-dessous permettent
de mettre en lumière la correspondance
entre
la phase (de
l'accumulateur de phase) et l'amplitude
(contenu en RAM) . C'est en quelque
sorte une conversion
phase vers amplitude.
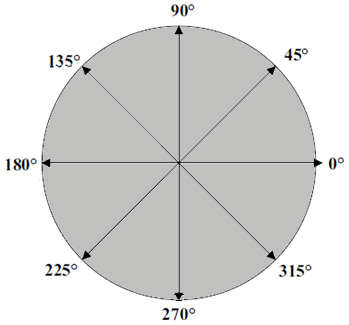
Sortie
de l'accumulateur de phase
si la
forme d'onde ne comporte que 8 points
de mesure
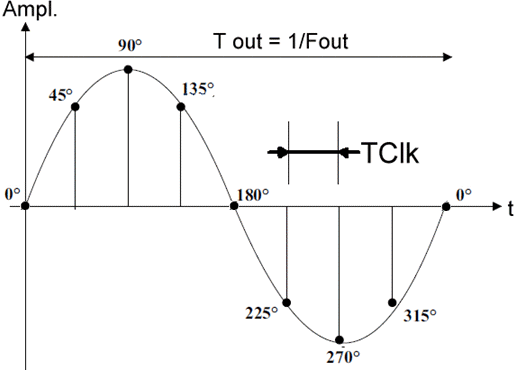
Sortie
de la RAM en correspondance
avec
la sortie de l'accumulateur de phase.
En
reprenant l'équation de la synthèse
numérique directe, on s'aperçoit
qu'une valeur de
M petite
induit de petits
sauts de phase
et par conséquent, une fréquence
générée en sortie
faible.
Inversement, une valeur grande
de M
permet de parcourir rapidement la totalité
de la phase
(360°) et la fréquence
de sortie est grande.
 Principe
du générateur de synthèse
numérique directe à circuits
TTL :
Principe
du générateur de synthèse
numérique directe à circuits
TTL :
Afin
de donner un exemple
concret de
la synthèse numérique
directe implanté dans le circuit
logique programme CPLD, voici un schéma
équivalent incomplet en logique
Fast-TTL de notre générateur
DDS.
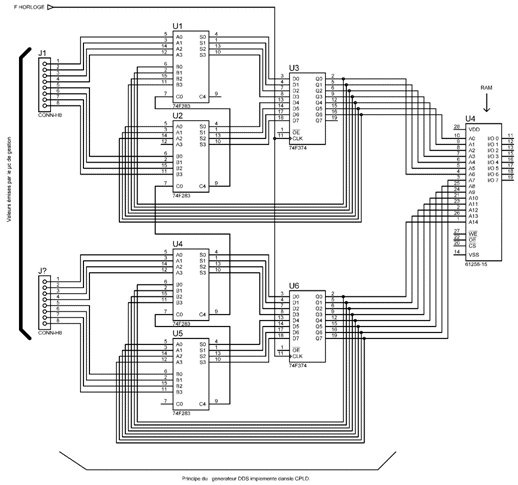
Cliquez sur l'image
ci-dessus pour l'agrandir
 Spectre
à la sortie du convertisseur
numérique - analogique et rôle
du filtre passe-bas : Spectre
à la sortie du convertisseur
numérique - analogique et rôle
du filtre passe-bas :
En
sortie du convertisseur numérique
- analogique nous retrouvons notre forme
d'onde représentative des octets
mémorisés dans la RAM.
Ci dessous, une sinusoïde composée
de quelques échantillons.
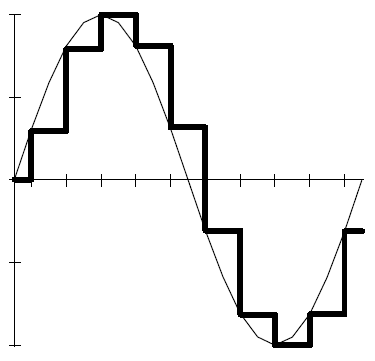
En
gras le signal présent
en sortie du CNA.
En trait fin, le
même signal après le filtrage
passe-bas.
Comme nous l'avons vu précédemment,
le filtre
passe-bas
permet de
lisser le signal mais aussi d'éliminer les
harmoniques
supérieurs
indésirables
générés par
l'échantillonnage du signal.
En effet le spectre
du
signal échantillonné
est caractérisés par
de multiples raies spectrales
délimitées par les
lobes d'un sinus cardinal (Sin
X / X) de sorte que l'amplitude
diminue lorsque la fréquence
augmente. Ainsi, le second rôle
du filtre
passe-bas est
donc de réduire
l'influence des raies spectrales parasites
à des niveaux acceptables.
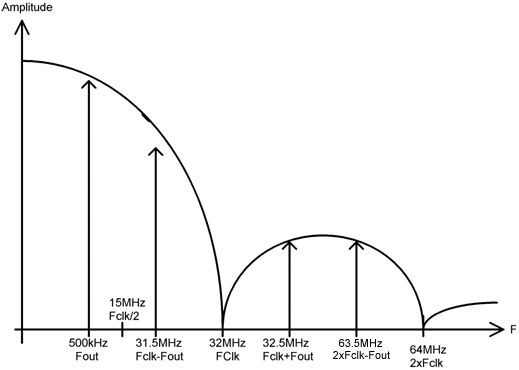
Prenons
par exemple une forme d'onde sinusoïdale
de fréquence Fout
=
500kHz
délivrée en sortie du
générateur. L'horloge
permettant de produire cette forme d'onde
est de Fclk
= 32MHz.
Le croquis ci-dessous met en lumière
les différentes raies
spectrales
avec : la
fondamentale à conserver
et les
parasites additionnels caractérisés
par les harmoniques
supérieurs que
l'on cherche à supprimer.
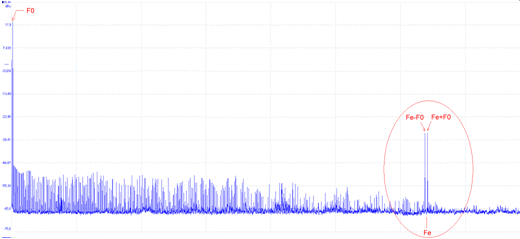
A
titre d'illustration, voici le spectre
réel
mesuré à l'analyseur de
spectre en sortie du générateur
dans les mêmes conditions qu'évoquées
précédemment lorsque le
filtre passe-bas est supprimé.
On note la présence des deux
premières raies parasites à
Fclk-Fout
et Fclk+Fout.
Cliquez sur l'image
ci-dessus pour l'agrandir
A
gauche du spectre, notre fondamentale à
Fout = 500kHz
et à droite nos deux premières raies à
Fclk-Fout
= 31.5MHz et
Fclk+Fout
= 32,5MHz.
Le
spectre réel met en lumière
d'autres composantes
parasites
qui sont introduites d'une part par
les
défauts de linéarité
du CNA
(erreurs de quantification, etc...)
et d'autre part par la résolution
du CNA limitée à 8 bits.
Afin de réduire au maximum ces
raies parasites secondaires, nous avons
choisi un CNA en technologie intégré
(TDA8702) conçu initialement
pour le traitement des
signaux rapides
tel que la vidéo-composite. Ainsi
de
part sa
vitesse de fonctionnement et
sa grande
linéarité,
le CNA utilisé minimise énormément
ces raies à des niveaux quasi-négligeables
(le filtre passe-bas les réduira
encore un peu plus).
En revanche,
si nous avions choisi un CNA à
réseau de résistances
pondérées de type R-2R,
le spectre du
signal de sortie disposerait de raies parasites d'amplitude bien
plus importantes et de ce fait, inacceptable
pour un tel instrument de laboratoire.
Par ailleurs, la linéarité
d'un tel CNA à réseau
de résistances reste
médiocre à moins de choisir
des résistances à 1%,
voire 0.1%.
 Fréquence
de coupure du filtre passe-bas : Fréquence
de coupure du filtre passe-bas :
Puisque
notre générateur de fonctions
balaye une large gamme de fréquence
(0,1Hz à 1MHz), il n'est donc
pas
possible d'utiliser un seul et unique
filtre passe-bas en sortie.
Ainsi, pour les 7
gammes
du générateur, il existe
7
filtres passe-bas dont
la fréquence de coupure a été
déterminée au plus juste.
De plus, vu
l'éloignement tout
relatif entre les premiers
harmoniques principaux
de notre forme d'onde produite
en sortie du générateur (excepté
pour une sinusoïde possédant
une seule raie)
et
la fréquence
de l'horloge,
un filtre passe-bas du
1er ordre suffit
amplement à éliminer les résidus
parasites que nous évoquions
précédemment.
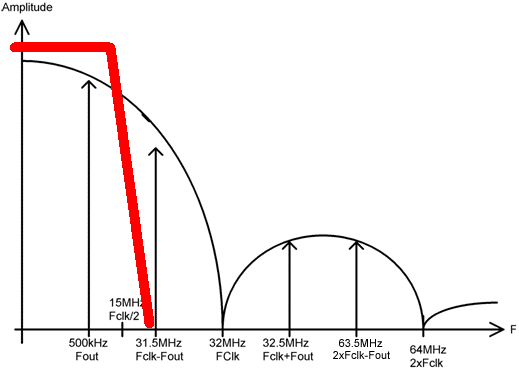
Voici la position
approximative
qu'occupe le filtre passe-bas
(en rouge)
pour réduire l'influence
des raies parasites.
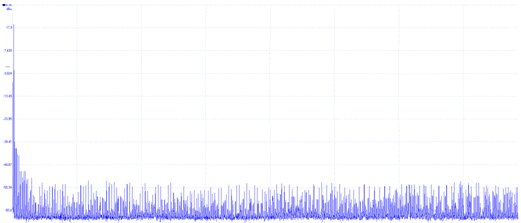
A
titre d'illustration, voici le spectre
réel
mesuré à l'analyseur de
spectre en sortie du générateur
dans les mêmes conditions qu'évoquées
précédemment lorsque le
filtre passe-bas est activé.
Les raies parasites sont
filtrées
tandis que nous pouvons observer le
plancher
de bruit lié
à la quantification du signal.
Toutefois la proportion de bruit reste
très inférieure
à notre signal proprement dit
dont la raie se situe à la fréquence
Fout.
Cliquez sur l'image
ci-dessus pour l'agrandir
Dans l'établissement
de la fréquence de coupure
des différents filtres deux
conditions impératives
doivent être respectées
pour un générateur de
forme d'onde numérique. La première
concerne l'élimination
des raies parasites
(voir chapitre précédent)
et la seconde concerne
l'allure du signal
en lui-même sur le plan temporel.
En effet, il faut faire en sorte que
le filtre passe-bas ne détériore
pas trop la
forme du signal présent en sortie. Pour une
forme d'onde sinusoïdale cela
ne pose aucun problème car son
spectre est représenté
par une
seule fondamentale.
En revanche, pour une forme
d'onde triangulaire (entre
autre...), sa transformée de
Fourrier nous indique qu'elle est composée
sur le plan fréquentiel d'une
fondamentale
et d'une infinité de raies aux
fréquences multiples de la fréquence
du fondamental.
Ainsi, si le filtre est mal déterminé,
on risque de supprimer les
principaux harmoniques de
notre forme d'onde triangulaire se traduisant
sur l'écran de l'oscilloscope
par un triangle aux allures d'une
sinusoïde déformée.
Ci-dessous
vous trouverez les différentes
fréquences de coupure des
7 filtres passe-bas
présents dans notre générateur.
Les fréquences de coupure ont
été déterminées
en premier lieu par calcul puis elles
furent ajustées en pratique au
cas par cas grâce à une visualisation directe
des signaux à l'oscilloscope.
|
Calibres
du générateur
|
Fréquence
de coupure
des 7 filtres
passe-bas
|
|
1Hz
|
40Hz
|
|
10Hz
|
100Hz
|
|
100Hz
|
330Hz
|
|
1kHz
|
10kHz
|
|
10kHz
|
60kHz
|
|
100kHz
|
850kHz
|
|
1MHz
|
15MHz
|
 Résolution
en fréquence du générateur
de fonctions de formes d'ondes arbitraires à
DDS :
Résolution
en fréquence du générateur
de fonctions de formes d'ondes arbitraires à
DDS :
L'aspect
de plus sensible de notre générateur
étant analysé dans les
grandes lignes, il ne nous reste plus
qu'à éclaircir un point
concernant la résolution en fréquence
de l'instrument. En effet, précédemment,
nous avons déterminé la
résolution
fréquentielle de notre générateur
DDS qui était de 1953Hz.
Or pour
générer toutes les fréquences
en sortie nous souhaiterions disposer d'une fréquence
d'horloge autres
que des multiples de 1953Hz,
afin par exemple de générer
les
plus basses fréquences de formes
d'ondes.
Pour
palier à ce problème,
la
solution repose tout simplement sur
la modification de
la table d'échantillons stockée
en RAM. En
effet, si l'on dilate
ou
l'on contracte
artificiellement
par
voie logicielle
une
onde composée d'échantillons,
on peut ainsi obtenir toutes les fréquences
souhaitées inférieures ou
supérieures
à la fréquence de résolution
du notre générateur DDS.
Certes, cette tâche est trop
complexe à intégrer dans
un microcontrôleur, mais en revanche un PC s'en tire
sans aucune difficulté. Ainsi,
c'est le logiciel du PC chargé
de gérer le générateur
qui va étirer
(réduire en fréquence)
ou qui raccourcir
(augmenter en fréquence) notre
forme d'onde que
l'on souhaite produire en sortie de
notre générateur. Les nouveaux
échantillons
représentatifs de la forme d'onde
"allongée"
ou "raccourcie"sont
ensuite programmés au sein de
la RAM. Ils sont relus à la cadence
de notre générateur DDS
à partir des
multiples de la résolution en
fréquence du
DDS afin d'obtenir une forme
d'onde à la fréquence
voulue.
|